#551. NOIP 2017 普及组初赛试题
NOIP 2017 普及组初赛试题
- 在 8 位二进制补码中,10101011 表示的数是十进制下的( )。 {{ select(1) }}
- 43
- -85
- -43
- -84
- 计算机存储数据的基本单位是( )。 {{ select(2) }}
- bit
- Byte
- GB
- KB
- 下列协议中与电子邮件无关的是( )。 {{ select(3) }}
- POP3
- SMTP
- WTO
- IMAP
- 分辨率为 800x600、16 位色的位图,存储图像信息所需的空间为( )。 {{ select(4) }}
- 937.5KB
- 4218.75KB
- 4320KB
- 2880KB
- 计算机应用的最早领域是( )。 {{ select(5) }}
- 数值计算
- 人工智能
- 机器人
- 过程控制
- 下列不属于面向对象程序设计语言的是( )。 {{ select(6) }}
- C
- C++
- JAVA
- C#
- NOI 的中文意思是( )。 {{ select(7) }}
- 中国信息学联赛
- 全国青少年信息学奥林匹克竞赛
- 中国青少年信息学奥林匹克竞赛
- 中国计算机协会
- 2017 年 10 月 1 日是星期日,1999 年 10 月 1 日是( )。 {{ select(8) }}
- 星期三
- 星期日
- 星期五
- 星期二
- 甲、乙、丙三位同学选修课程,从 4 门课程中,甲选修 2 门,乙、丙各选修3门,则不同的选修方案共有( )种。 {{ select(9) }}
- 36
- 48
- 96
- 192
- 设 G 是有 n 个结点、m 条边(n ≤ m)的连通图,必须删去 G 的( )条边,才能使得 G 变成一棵树。 {{ select(10) }}
- m – n + 1
- m - n
- m + n + 1
- n – m + 1
- 对于给定的序列{ak},我们把 (i, j) 称为逆序对当且仅当 i < j 且 ai > aj。那么 序列 1, 7, 2, 3, 5, 4 的逆序对数为( )个。 {{ select(11) }}
- 4
- 5
- 6
- 7
- 表达式 a * (b + c) * d 的后缀形式是( )。 {{ select(12) }}
- a b c d * + *
- a b c + * d *
- a * b c + * d
- b + c * a * d
- 向一个栈顶指针为 hs 的链式栈中插入一个指针 s 指向的结点时,应执行( )。 {{ select(13) }}
- hs->next = s;
- s->next = hs; hs = s;
- s->next = hs->next; hs->next = s;
- s->next = hs; hs = hs->next;
- 若串 S = “copyright”,其子串的个数是( )。 {{ select(14) }}
- 72
- 45
- 46
- 36
- 十进制小数 13.375 对应的二进制数是( )。 {{ select(15) }}
- 1101.011
- 1011.011
- 1101.101
- 1010.01
- 对于入栈顺序为 a, b, c, d, e, f, g 的序列,下列( )不可能是合法的出栈序列。 {{ select(16) }}
- a, b, c, d, e, f, g
- a, d, c, b, e, g, f
- a, d, b, c, g, f, e
- g, f, e, d, c, b, a
- 设 A 和 B 是两个长为 n 的有序数组,现在需要将 A 和 B 合并成一个排好序的数组,任何以元素比较作为基本运算的归并算法在最坏情况下至少要做( )次比较。 {{ select(17) }}
- n log n
- 2n
- 2n - 1
- 从( )年开始,NOIP 竞赛将不再支持 Pascal 语言。 {{ select(18) }}
- 2020
- 2021
- 2022
- 2023
- 一家四口人,至少两个人生日属于同一月份的概率是( )(假定每个人生日属于每个月份的概率相同且不同人之间相互独立)。 {{ select(19) }}
- 1/12
- 1/144
- 41/96
- 3/4
- 以下和计算机领域密切相关的奖项是( )。 {{ select(20) }}
- 奥斯卡奖
- 图灵奖
- 诺贝尔奖
- 普利策奖
-
第21题 一个人站在坐标(0, 0)处,面朝 x 轴正方向。第一轮,他向前走 1 单位距离,然后右转;第二轮,他向前走 2 单位距离,然后右转;第三轮,他向前走 3 单位距离,然后右转……他一直这么走下去。请问第 2017 轮后,他的坐标是:( _________ , _________ )。(请在答题纸上用逗号隔开两空答案)

{{ input(21) }}
-
第22题 如下图所示,共有 13个格子。对任何一个格子进行一次操作,会使得它自己以及与它上下左右相邻的格子中的数字改变(由 1变 成0,或由 0变成1)。现在要使得所有的格子中的数字都变为 0,至少需要_________次操作。
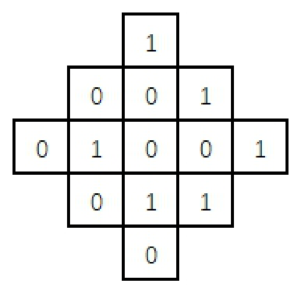
{{ input(22) }}
-
第23题
** 阅读程序写结果: **
#include <iostream>
using namespace std;
int main()
{
int t[256];
string s;
int i;
cin >> s;
for (i = 0; i < 256; i++)
t[i] = 0;
for (i = 0; i < s.length(); i++)
t[s[i]]++;
for (i = 0; i < s.length(); i++)
if (t[s[i]] == 1)
{
cout << s[i] << endl;
return 0;
}
cout << "no" << endl;
return 0;
}
输入:xyzxyw
输出:_________
{{ input(23) }}
- 第24题
** 阅读程序写结果: **
#include<iostream>
using namespace std;
int g(int m, int n, int x)
{
int ans = 0;
int i;
if (n == 1)
return 1;
for (i = x; i <= m / n; i++)
ans += g(m - i, n - 1, i);
return ans;
}
int main()
{
int t, m, n;
cin >> m >> n;
cout << g(m, n, 0) << endl;
return 0;
}
输入:7 3
输出:_________
{{ input(24) }}
- 第25题
** 阅读程序写结果: **
#include<iostream>
using namespace std;
int main()
{
string ch;
int a[200];
int b[200];
int n, i, t, res;
cin >> ch;
n = ch.length();
for (i = 0; i < 200; i++)
b[i] = 0;
for (i = 1; i <= n; i++)
{
a[i] = ch[i - 1] - '0';
b[i] = b[i - 1] + a[i];
}
res = b[n];
t = 0;
for (i = n; i > 0; i--)
{
if (a[i] == 0)
t++;
if (b[i - 1] + t < res)
res = b[i - 1] + t;
}
cout << res << endl;
return 0;
}
输入:1001101011001101101011110001
输出:_________
{{ input(25) }}
- 第26题
** 阅读程序写结果: **
#include<iostream>
using namespace std;
int main()
{
int n, m;
cin >> n >> m;
int x = 1;
int y = 1;
int dx = 1;
int dy = 1;
int cnt = 0;
while (cnt != 2)
{
cnt = 0;
x = x + dx;
y = y + dy;
if (x == 1 || x == n)
{
++cnt;
dx = -dx;
}
if (y == 1 || y == m)
{
++cnt;
dy = -dy;
}
}
cout << x << " " << y << endl;
return 0;
}
输入 1:4 3
输出 1:_________(3 分)
输入 2:2017 1014
输出 2:_________(5 分)
1.{{ input(26) }}
2.{{ input(27) }}
- 第27题
完善程序: (快速幂) 请完善下面的程序,该程序使用分治法求mod m 的值。(第一空 2 分,其余 3 分)
输入:三个不超过 10000 的正整数 x,p,m。 输出:mod m 的值。 提示:若 p为偶数,;若为奇数,
#include<iostream>
using namespace std;
int x, p, m, i, result;
int main(){
cin >> x >> p >> m;
result = ①;
while (②){
if (p % 2 == 1)
result = ③;
p /= 2;
x = ④;
}
cout << ⑤ << endl;
return 0;
}
- {{ select(110) }}
- 1
- 2
- 3
- 4
- {{ select(111) }}
- p>0
- p>=0
- p<0
- p<=0
- {{ select(112) }}
- result * x % m
- result * x % m-1
- result * x % m-2
- result * x % m-3
4.{{ select(113) }}
- x * x % m
- x * x % m-1
- x * x % m-3
- x * x % n
- {{ select(114) }}
- result
- n
- m
- k
- 第28题
完善程序: (切割绳子) 有 n 条绳子,每条绳子的长度已知且均为正整数。绳子可以以任意正整数长度切割,但不可以连接。现在要从这些绳子中切割出 m 条长度相同的绳段,求绳段的最大长度是多少。(第一、二空 2.5 分,其余 3 分)
输入:第一行是一个不超过 100 的正整数 n,第二行是 n 个不超过的正整数,表示每条绳子的长度,第三行是一个不超过的正整数 m。 输出:绳段的最大长度,若无法切割,输出 Failed 。
#include<iostream>
using namespace std;
int n, m, i, lbound, ubound, mid, count;
int len[100]; // 绳子长度
int main()
{
cin >> n;
count = 0;
for (i = 0; i < n; i++)
{
cin >> len[i];
①;
}
cin >> m;
if (②)
{
cout << "Failed" << endl;
return 0;
}
lbound = 1;
ubound = 1000000;
while (③)
{
mid = ④;
count = 0;
for (i = 0; i < n; i++)
⑤;
if (count < m)
ubound = mid - 1;
else
lbound = mid;
}
cout << lbound << endl;
return 0;
}
- {{ select(120) }}
- count=count+len[i]
- count=count+len[i-1]
- count=count+1+len[i]
- count=len[i]
- {{ select(121) }}
- count<=m
- count>=m
- count<m
- count==m
- {{ select(122) }}
- lbound<ubound
- lbound<=ubound
- lbound>ubound
- lbound>=ubound
4.{{ select(123) }}
- (lbound+ubound+1)/2
- (lbound+ubound+1)/3
- (lbound+ubound+1)/4
- (lbound+ubound+1)/5
- {{ select(124) }}
- count=count+len[i]/mid
- count=count+len[i]/mid-1
- count=count+len[i]/mid-2
- count=count+len[i]/mid-3
